ScyllaDB, being a database able to maintain exabytes of data and provide millions of operations, has to maximize utility of all available hardware resources including CPU, memory, plus disk and network IO. According to its data model ScyllaDB needs to maintain a set of partitions, rows and cell values providing fast lookup, sorted scans and keeping the memory consumption as low as possible. One of the core components that greatly affects ScyllaDB’s performance is the in-memory cache of the user data (we call it the row cache). And one of the key factors to achieving the performance goal is a good selection of collections — the data structures used to maintain the row cache objects. In this blog post I’ll try to demonstrate a facet of the row cache that lies at the intersection of academic computer-science and practical programming — the trees.
In its early days, ScyllaDB used standard implementations of key-value maps that were Red-Black (RB) trees behind the scenes. Although the standard implementation was time-proven to be stable and well performing, we noticed a set of performance-related problems with it: memory consumption could have been better, tree search seemed to take more CPU power than we expected it to, and some design ideas that were considered to be “corner case” turned out to be critical for us. The need for a better implementation arose and, as a part of this journey, we had to re-invent the trees again.
To B- or Not to B-Tree
An important characteristic of a tree is called cardinality. This is the maximum number of child nodes that another node may have. In the corner case of cardinality of two, the tree is called a binary tree. For other cases, there’s a wide class of so-called B-trees. The common belief about binary vs B- trees is that the former ones should be used when the data is stored in the RAM, whilst the latter trees should live in the disk. The justification for this split is that RAM access speed is much higher than disk. Also, disk IO is performed in blocks, so it’s much better and faster to fetch several “adjacent” keys in one request. RAM, unlike disks, allows random access with almost any granularity, so it’s OK to have a disperse set of keys pointing to each other.
However, there are many reasons why B-trees are often a good choice for in-memory collections.The first reason is cache locality. When searching for a key in a binary tree, the algorithm would visit up to logN elements that are very likely dispersed in memory. On a B-tree, this search will consist of two phases — intra-node search and descending the tree — executed one after another. And while descending the tree doesn’t differ much from the binary tree in the aforementioned sense, intra-node search will access keys that are located next to each other, thus making much better use of CPU caches.
The second reason also comes from the dispersed nature of binary trees and from how modern CPUs are designed. It’s well known that when executing a stream of instructions, CPU cores split the processing of each instruction into stages (loading instructions, decoding them, preparing arguments and doing the execution itself) and the stages are run in parallel in a unit called a conveyor. When a conditional branching instruction appears in this stream, the conveyor needs to guess which of two potential branches it will have to execute next and start loading it into the conveyor pipeline. If this guess fails, the conveyor is flushed and starts to work from scratch. Such failures are called branch misprediction. They are very bad from the performance point of view and have direct implications on the binary search algorithm. When searching for a key in such a tree, the algorithm jumps left and right depending on the key comparison result without giving the CPU any chance to learn which direction is “preferred.” In many cases, the CPU conveyer is flushed.
The two-phased B-tree search can be made better with respect to branch predictions. The trick is in making the intra-node search linear, i.e. walking the array of keys forward key-by-key. In this case, there will be only a “should we move forward” condition that’s much more predictable. There’s even a nice trick of turning binary search into linear without sacrificing the number of comparisons.
Linear Search on Steroids
That linear search can be improved a bit more. Let’s count carefully the number of key comparisons that it may take to find a single key in a tree. For a binary tree, it’s well known that it takes log2N comparisons (on average) where N is the number of elements. I put the logarithm base here for a reason. Next, let’s consider a k-ary tree with k kids per node. Does it take less comparisons? (Spoiler: no). To find the element, we have to do the same search — get a node, find in which branch it sits, then proceed to it. We have logkN levels in the tree, so we have to do that many descending steps. However on each step we need to do the search within k elements which is, again, log2k if we’re doing a binary search. Multiplying both, we still need at least log2N comparisons.
The way to reduce this number is to compare more than one key at a time when doing intra-node search. In case keys are small enough, SIMD instructions can compare up to 64 keys in one go. Although a SIMD compare instruction may be slower than a classic cmp one and requires additional instructions to process the comparison mask, linear SIMD-powered search wins on short enough arrays (and B-tree nodes can be short enough). For example, here are the times of looking up an integer in a sorted array using three techniques — linear search, binary search and SIMD-optimized linear search such as the x86 Advanced Vector Extensions (AVX).
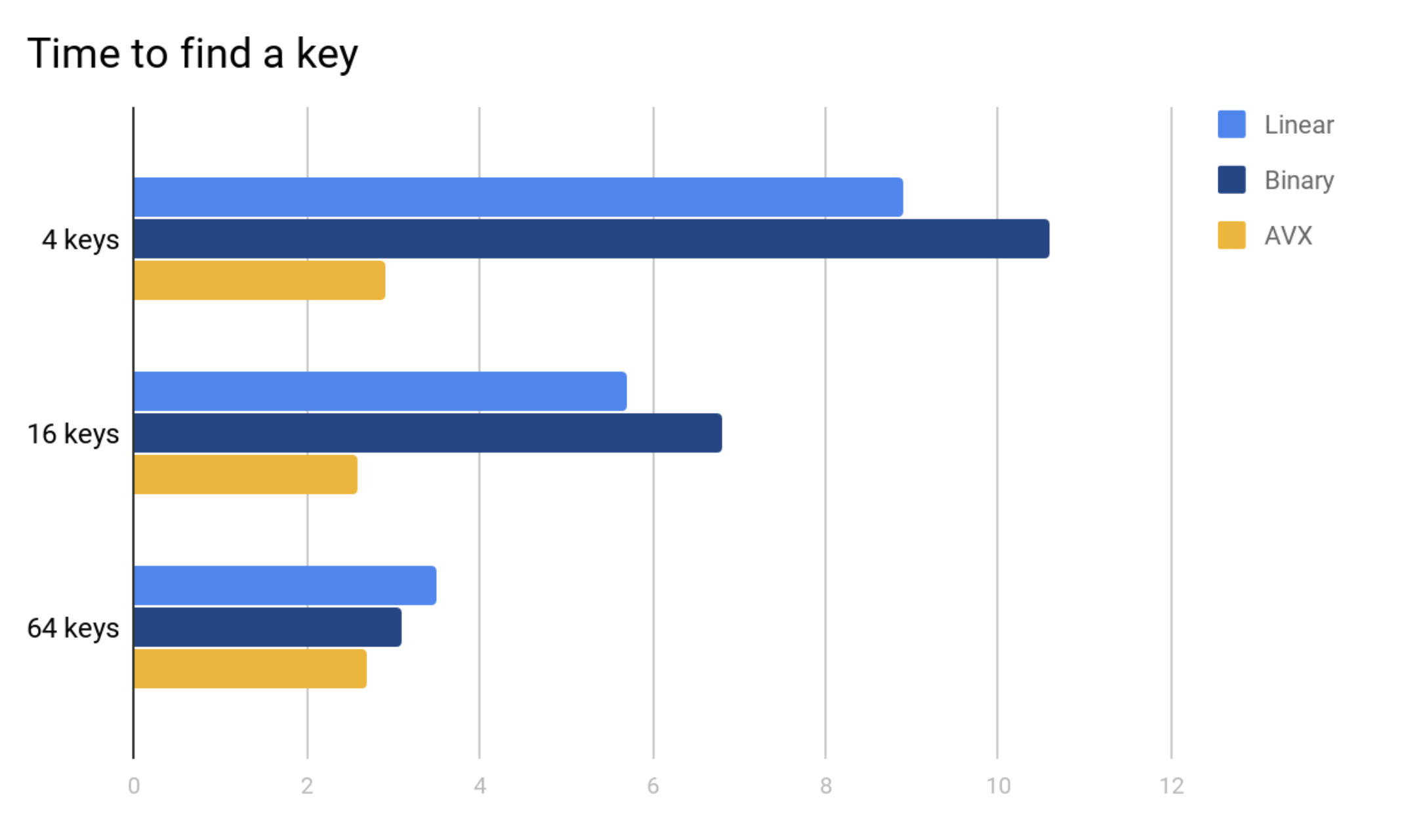
The test used a large amount of randomly generated arrays of values dispersed in memory to eliminate differences in cache usage and a large amount of random search keys to blur branch predictions. Shown above are the average times of finding a key in an array normalized by the array length. Smaller results are faster (better).
Scanning the Tree
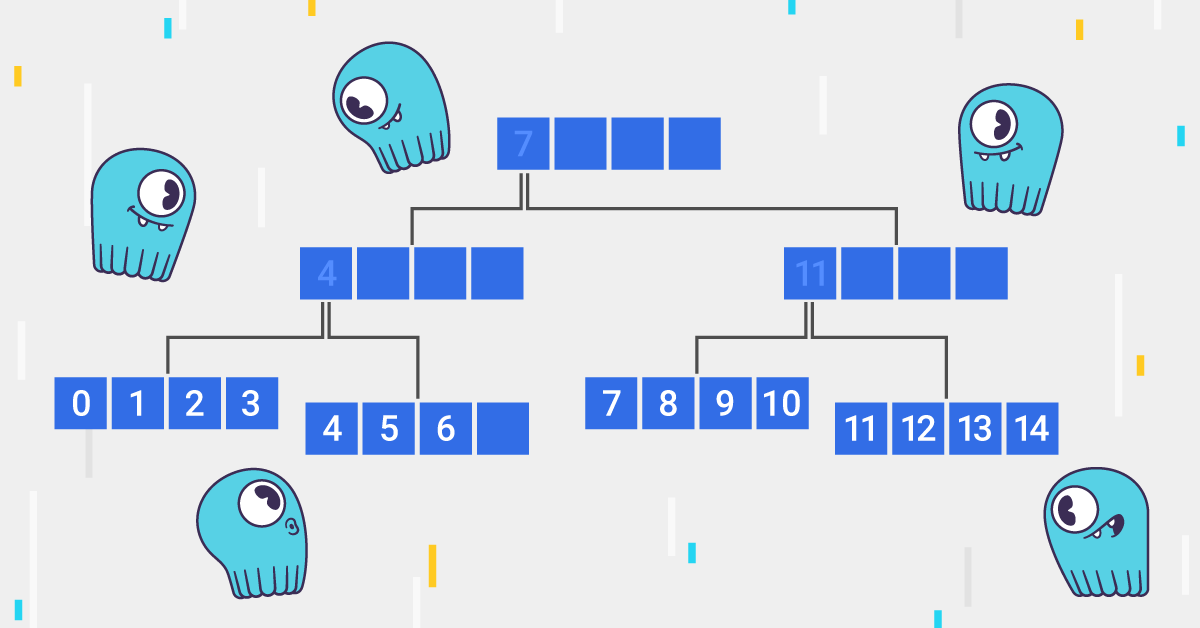
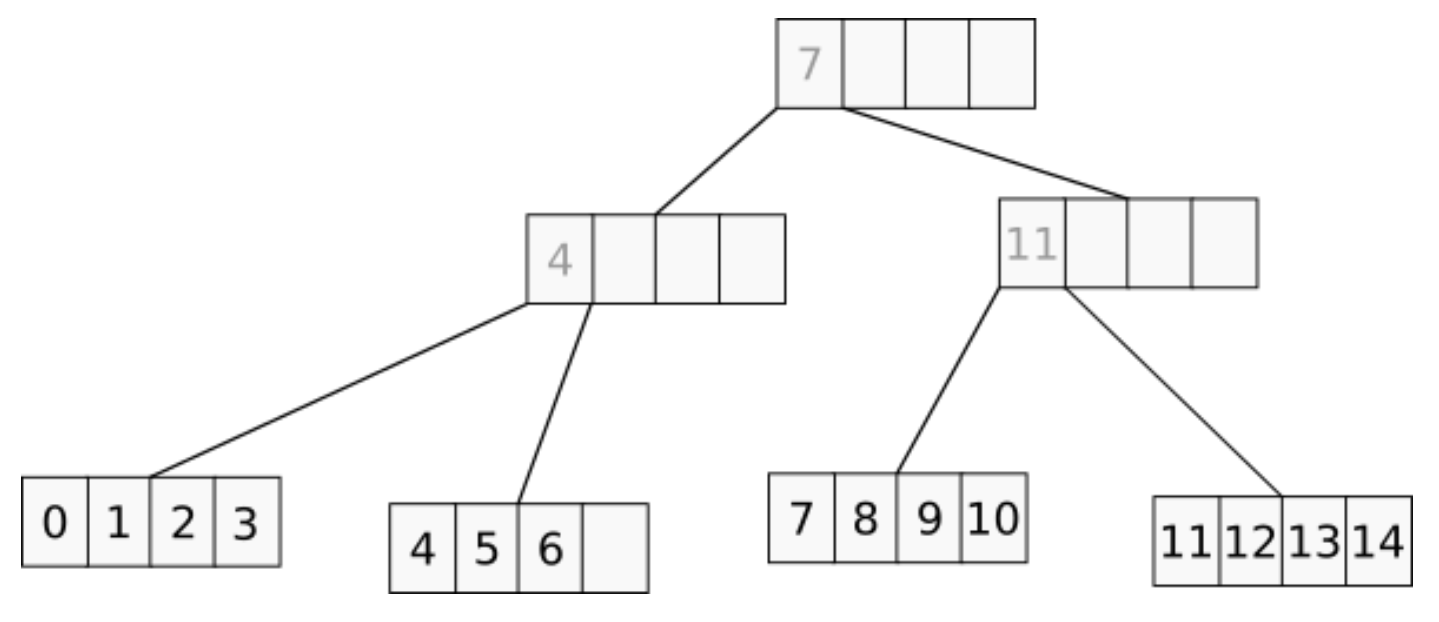
One interesting flavor of B-trees is called a B+-tree. In this tree, there are two kinds of keys — real keys and separation keys. The real keys live on leaf nodes, i.e. on those that don’t have child ones, while separation keys sit on inner nodes and are used to select which branch to go next when descending the tree. This difference has an obvious consequence that it takes more memory to keep the same amount of keys in a B+-tree as compared to B-tree, but it’s not only that.
A great implicit feature of a tree is the ability to iterate over elements in a sorted manner (called scan below). To scan a classical B-tree, there are both recursive and state-machine algorithms that process the keys in a very non-uniform manner — the algorithm walks up-and-down the tree while it moves. Despite B-trees being described as cache-friendly above, scanning it needs to visit every single node and inner nodes are visited in a cache unfriendly manner.
Opposite to this, B+-trees’ scan only needs to loop through its leaf nodes, which, with some additional effort, can be implemented as a linear scan over a linked list of arrays.
When the Tree Size Matters
Talking about memory, B-trees don’t provide all the above benefits for free (neither do B+-trees). As the tree grows, so does the number of nodes in it and it’s useful to consider the overhead needed to store a single key. For a binary tree, the overhead would be three pointers — to both left and right children as well as to the parent node. For a B-tree, it will differ for inner and leaf nodes. For both types, the overhead is one parent pointer and k pointers to keys, even if they are not inserted in the tree. For inner nodes there will be additionally k+1 pointers to child nodes.
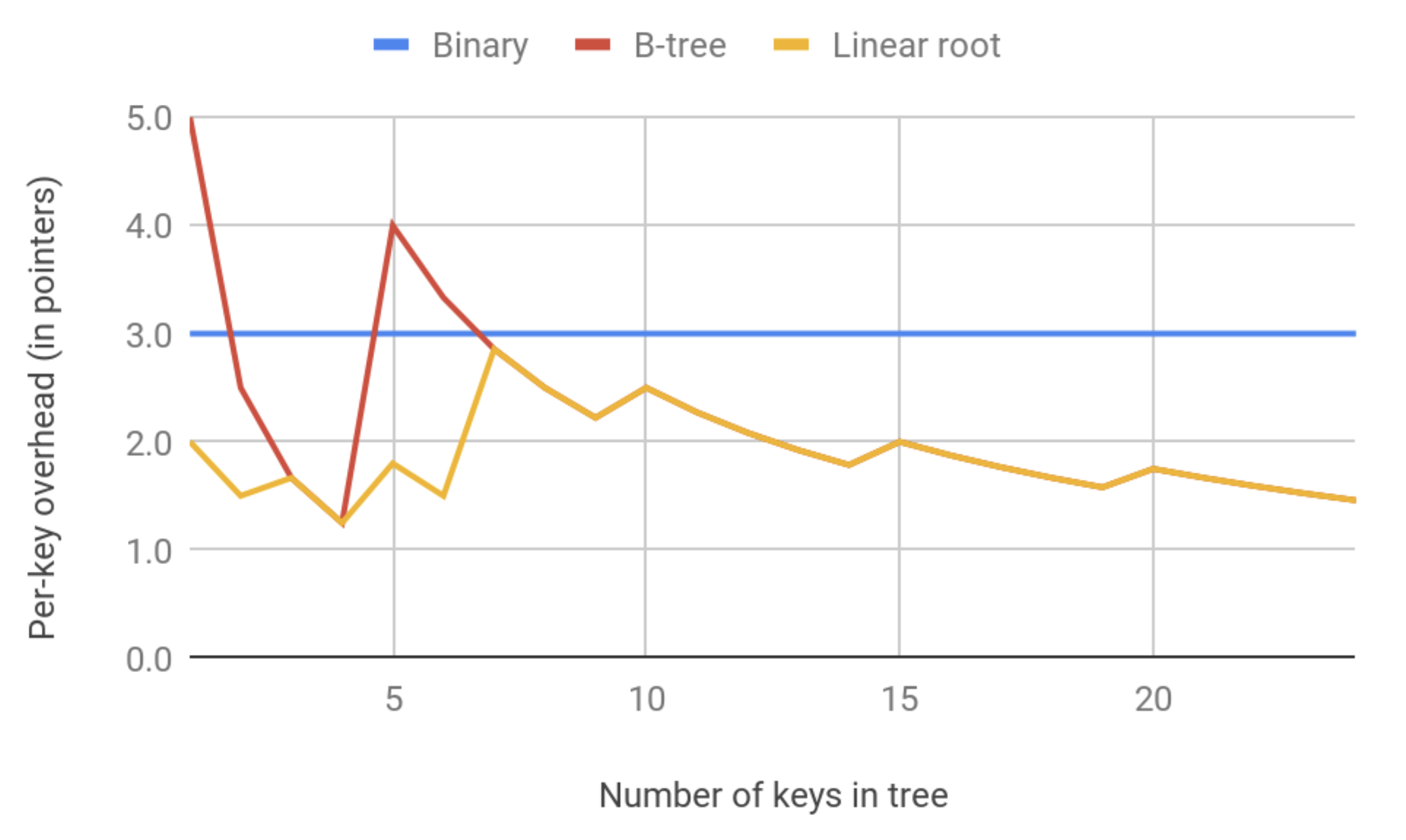
The number of nodes in a B-tree is easy to estimate for a large number of keys. As the number of nodes grows, the per-key overhead blurs as keys “share” parent and children pointers. However, there’s a very interesting point at the beginning of a tree’s growth. When the number of keys becomes k+1 (i.e. the tree overgrows its first leaf node), the number of nodes jumps three times because, in this case, it’s needed to allocate one more leaf node and one inner node to link those two.
There is a good and pretty cheap optimization to mitigate this spike that we’ve called “linear root.” The leaf root node grows on demand, doubling each step like a std::vector in C++, and can overgrow the capacity of k up to some extent. Shown on the graph below is the per-key overhead for a 4-ary B-tree with 50% initial overgrow. Note the first split spike of a classical algorithm at 5 keys.
If talking about how B-trees work with small amounts of keys, it’s worth mentioning the corner case of 1 key. In ScyllaDB, a B-tree is used to store clustering rows inside a partition. Since it’s allowed to have a schema without a clustering key, it’s thus possible to have partitions that always have just one row inside, so this corner case is not that “corner” for us. In the case of a binary tree, the single-element tree is equivalent to having a direct pointer from the tree owner to this element (plus the cost of two nil pointers to the left and right children). In case of a B-tree, the cost of keeping the single key is always in having a root node that implies extra pointer fetching to access this key. Even the linear root optimization is helpless here. Fixing this corner case was possible by re-using the pointer to the root node to point directly to the single key.
The Secret Life of Separation Keys
Next, let’s dive into technical details of B+-tree implementation — the practical information you won’t read in books.
There are two different ways of managing separation keys in a B+-tree. The separation key at any level must be less than or equal to all the keys from its right subtree and greater than or equal to all the keys from its left subtree. Mind the “or” condition — the exact value of the separation key may or may not coincide with the value of some key from the respective branch (it’s clear that this some will be the rightmost key on the left branch or leftmost on the right). Let’s name these two cases. If the tree balancing maintains the separation key to be independent from other key values, then it’s the light mode; if it must coincide with some of them, then it will be called the strict mode.
In the light separation mode, the insertion and removal operations are a bit faster because they don’t need to care about separation keys that much. It’s enough if they separate branches, and that’s it. A somewhat worse consequence of the light separation is that separation keys are separate values that may appear in the tree by copying existing keys. If the key is simple, e.g. an integer, this will likely not cause any troubles. However, if keys are strings or, as in ScyllaDB’s case, database partition or clustering keys, copying it might be both resource consuming and out-of-memory risky.
On the other hand, the strict separation mode makes it possible to avoid keys copying by implementing separation keys as references on real ones. This would involve some complication of insertion and especially removal operations. In particular, upon real key removal it will be needed to find and update the relevant separation keys. Another difficulty to care about is that moving a real key value in memory, if it’s needed (e.g. in ScyllaDB’s case keys are moved in memory as a part of memory defragmentation hygiene), will also need to update the relevant reference from separation keys. However, it’s possible to show that each real key will be referenced by at most one separation key.
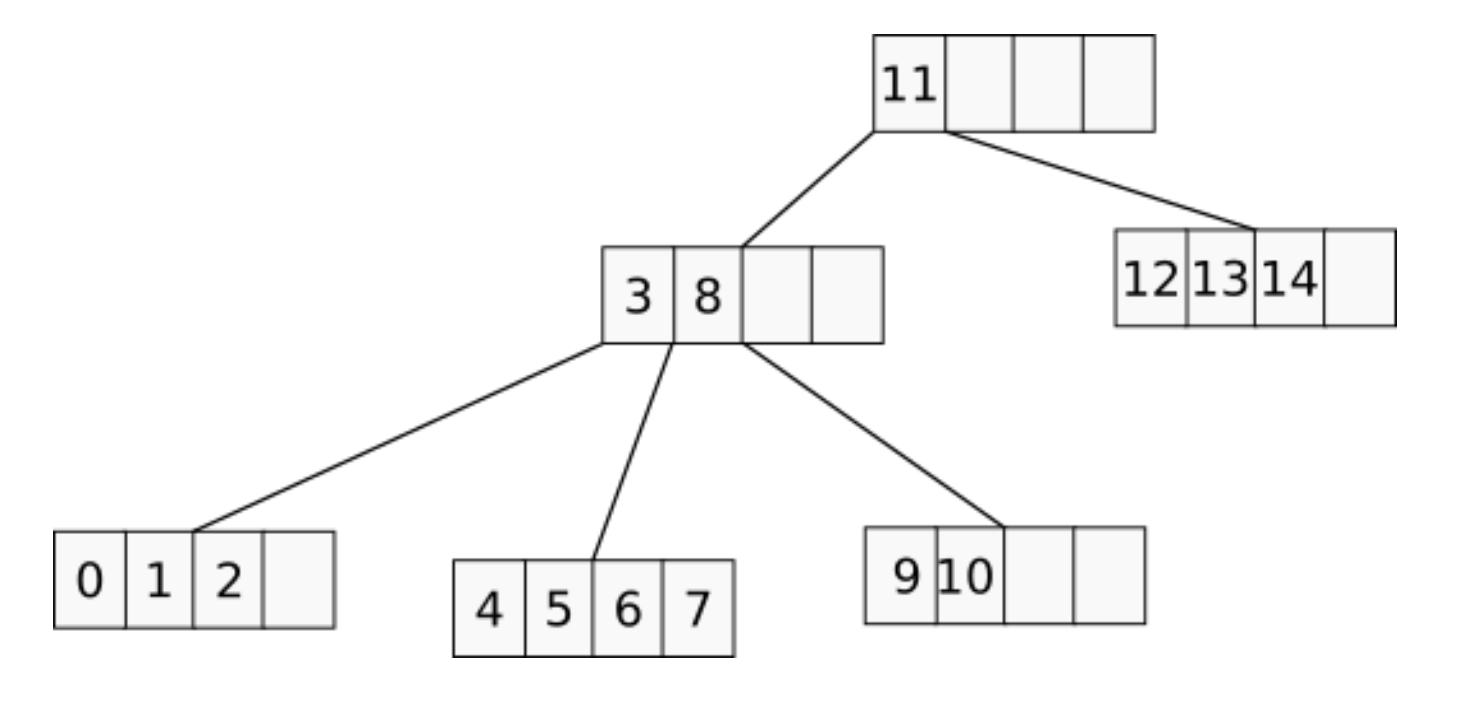
Speaking about memory consumption… although large B-trees were shown to consume less memory per-key as they get filled, the real overhead would very likely be larger, since the nodes of the tree will typically be underfilled because of the way the balancing algorithm works. For example, this is how nodes look like in a randomly filled 4-ary B-tree:
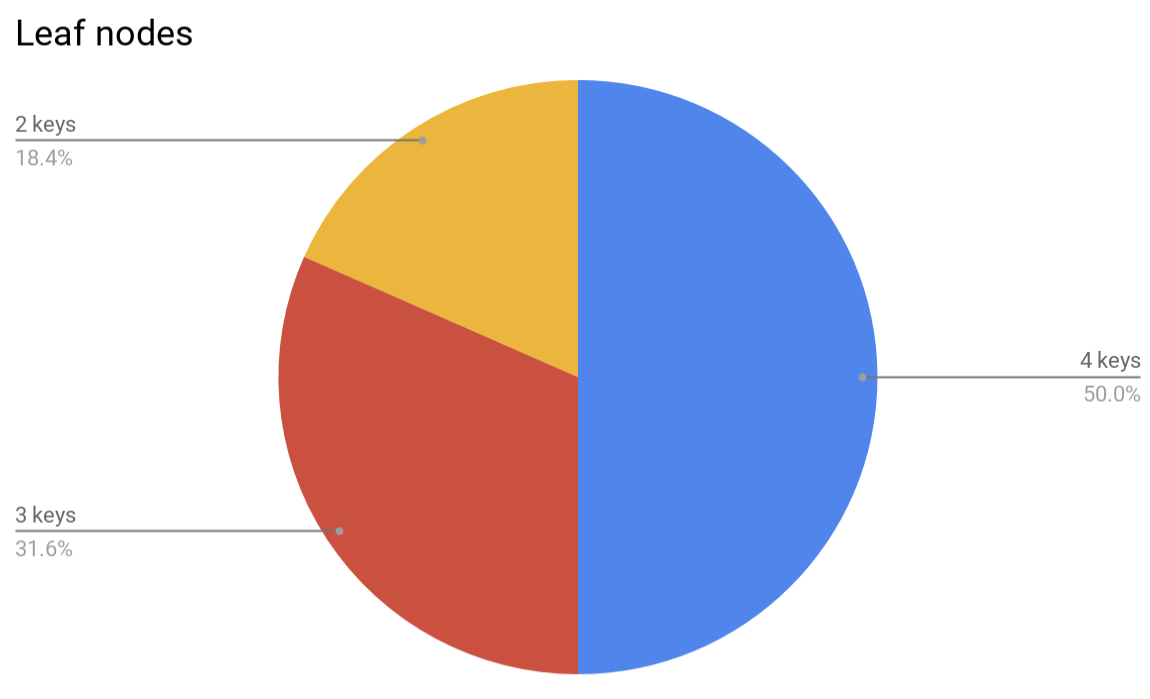
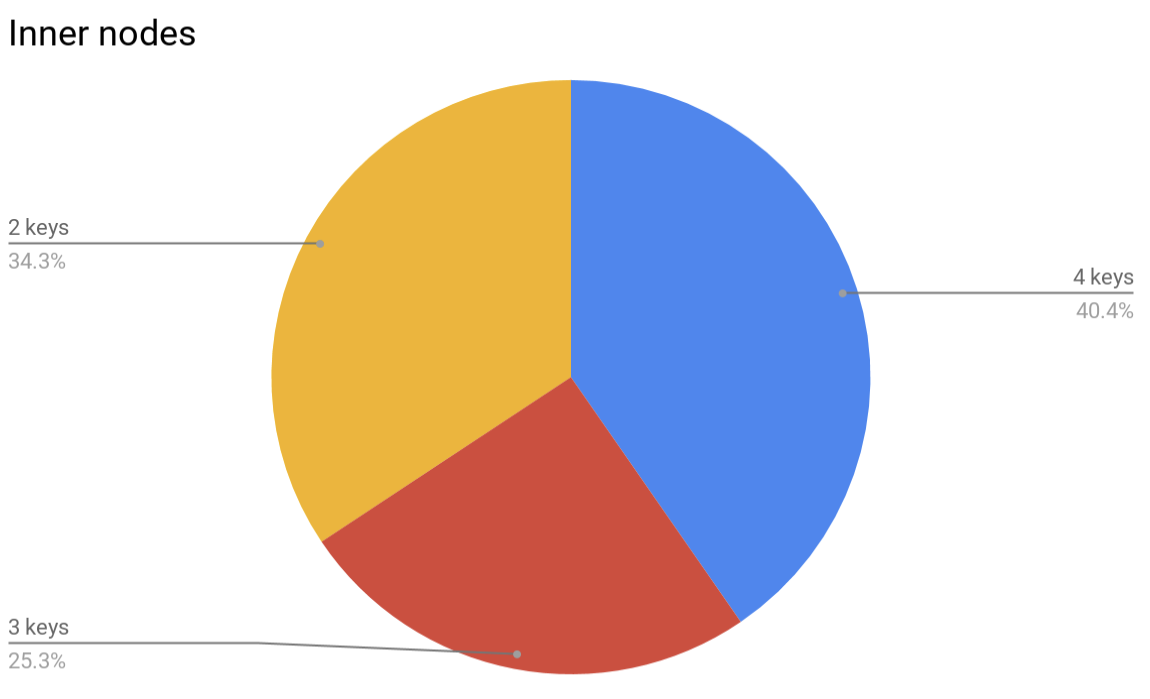
It’s possible to define a compaction operation for a B-tree that will pick several adjacent nodes and squash them together, but this operation has its limitations. First, a certain amount of under-occupied nodes makes it possible to insert a new element into a tree without the need to rebalance, thus saving CPU cycles. Second, since each node cannot contain less than a half of its capacity, squashing 2 adjacent nodes is impossible, even if considering three adjacent nodes then the amount of really squashable nodes would be less than 5% of leaves and less than 1% of inners.
Conclusions
In this blog post, I’ve only touched on the most prominent aspects of adopting B- and B+- trees for in-RAM usage. Lots of smaller points were tossed overboard for brevity — for example the subtle difference in odd vs even number of keys on a node. This exciting journey proved one more time that the exact implementation of an abstract math concept is very very different from its on-paper model.
B+-trees have been supported since ScyllaDB Open Source 4.3, and our B-tree implementation was added in release 4.5. They are hidden, under-the-hood optimizations ScyllaDB users benefit from as we continue to evolve our infrastructure.